PROPORCIONALIDAD DE MAGNITUDES

Vamos a ver un vídeo que te explica algunos conceptos importantes para aprender los que llamamos PROPORCIONALIDAD.

INICIACIÓN A LOS TANTOS POR CIENTO

Cuando decimos que el 65% del peso del cuerpo humano (aproximadamente) es agua, queremos decir que si la persona pesa 100 kilos, unos 65kilos correspondería al agua y los 35 kilos restantes al resto de componentes del cuerpo.

Cuando decimos el un equipo de baloncesto tiene un 80% de acierto en los tiros libres es que si tirara 100 veces acertaría 80, pero de igual manera...
- si tirara 10 veces... acertaría 8
- si tirara 20 veces... acertaría 16
- si tirara 50 veces acertaría 40
- si tirara 200 veces acertaría 160
....

Vamos a ver dos formas de calcular el % de una cantidad.
Por ejemplo vamos a calcular el 20% de 300.

a) Como una fracción.
El 20% equivale a la fracción 20/100, por lo que...
20% de 300 = 20·300/100 = 60

b) Como un número decimal.
El 20% equivale a la fracción 20/100 que a su vez es el número 0,20, por lo que...
20% de 300 = 0,20 · 300 = 60

A continuación tienes unos ejercicios sencillos de cálculo y resolución de problemas mediante tantos por ciento:

Vamos a estudiar cinco tipos de problemas…

a)      Calculo del resultado

Tengo 600€ y he gastado el 30% en una bicicleta. ¿Cuánto me ha costado la bicicleta?

Calcularíamos el 30% de 600€ …

600 : 100 · 30 = 180

O también:
600 · 0.30 = 180

Respuesta: Me ha costado 180€

b)      Calculo del %

Tengo 600€ y me he gastado 180€ en una bicicleta. ¿Qué % supone ese gasto?

Formaríamos la fracción: parte que gasté / dinero total que tenía, y luego...
180/600 = 3/10 = 0,30 = 30/100 = 30%

O también; 
180/600 = x/100

Para que esa igualdad sea cierta…

600·x =180·100

600x=18000

6x=180

6x/6=180/6

x=30

Respuesta: Supone un gasto del 30%

c)       Cálculo del total

Me he gastado 180€ en una bicicleta, lo que supone el 30% del dinero que tengo. ¿Cuánto dinero tenía?

30% del dinero que tengo = 180€

180 : 30 · 100 = 600

Respuesta: Tengo 600€.

O también:
180: 0.30 = 600

Respuesta: Tenía 600€

d)      Disminución porcentual o rebaja.

Al comprar un abrigo de 400€ me han aplicado una rebaja del 25%. ¿Cuánto he tenido que pagar?

100% - 25% de rebaja = 75% de pago

75% de 400€ = 75·400/100 = 300€

Respuesta: Tendré que pagar 300€.

e)      Aumento porcentual o recargo.

Me han puesto una multa de 500€ y por no pagarla en el plazo estipulado me han aplicado una una penalización añadida del 20%. ¿Cuánto tendré que pagar?

100% + 20% de penalización=120%

120% de 500€ = 120·500/100 = 600€

Respuesta: Tendré que pagar 600€.

Una aplicación de los descuentos y recargos los tenemos en las facturas. Aquí tienes un modelo:

Resultados OFERTA RARILLA

He realizado una tabla para contestar a las preguntas que se nos hacía.

Si comparamos "la gran oferta" de este supermercado nos damos cuenta:

- Que el precio de partida de la lata es de 0,75€, es decir 20 céntimos más que en el otro... 

- Qué con la oferta del -50% en la segunda unidad, además de tener que comprar dos nos sale todavía más caro.

- Que con la oferta del -70% si nos sale más barato (6 céntimos), pero necesitamos comprar dos latas, es decir gastar 0,98€ en dos latas vez de gastar 0,55€ en una sola lata.

ESTUDIO DE UNA OFERTA RARILLA...

Hoy he visto esta oferta real en un comercio. Me parece un poco liosa dado que en la oferta aparecen varias cifras, aparecen dos tipos de ofertas, aparecen las cifras en distintos tamaños y colores...
En defintiva, al final no la compré porque no me pareció tan barato.  Pero creo interesante verla con atención.

Me podrías decir...
a) ¿Cuanto me costaría una cerveza?
b) ¿Cuánto me costaría una cerveza con la oferta de la segunda al -50%?
c) ¿Cuánto me costarían dos cervezas con la oferta de la segunda al -50%?
d) ¿Cuánto me costaría una cerveza con la oferta cupón de la segunda al -70%?
e) ¿Cuánto me costarían dos cervezas con la oferta cupón de la segunda al -70%?
f) ¿Cuánto me costarían dos paquetes de cuatro cervezas con la mejor opción?
g) ¿Cuánto me costarían tres cervezas con la mejor opción?
h) ¿Crees que las operaciones están bien calculadas en la oferta?

Luego me ha picado la curiosidad y he visto su precio en otro supermercado...

... ¿Qué piensas después de haber realizado todos los cálculos anteriores?

RESULTADOS ESTUDIO COMPARATIVO DE OFERTAS

OFERTAS, OFERTAS, OFERTAS...

Imagina que vamos a una tienda en la que un perfume vale 10€ y nos indican que tienen la siguiente oferta:

"Llévese cuatro y pague tres" , 

es decir, sería lo mismo que...

"De cada cuatro que se lleve no pague uno"

Calcularíamos que:
La fracción sería 10/40 = 1/4 = 0.25 = 25% de rebaja;

eso sí, para que nos hagan la rebaja 
tendríamos que comprar cuatro perfumes

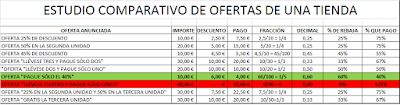
Otro día, en esa misma tienda nos dan hasta nueve posibilidades de oferta para acogernos...

Calcula qué tanto por ciento de oferta real te está ofreciendo cada una de ellas para que puedas compararlas.

Para ello te propongo que trabajes con el cuaderno apaisado y que utilices la siguiente tabla:

Magnitudes

	Magnitud	Instrumentos de medida	Unidades de medida
1	La temperatura. Mide lo caliente o frío que está un objeto	Termómetros	Grados Celsius (º C) Grados Kelvin (º K)
2	La longitud. Mide el largo, o el ancho, o el alto de un objeto o la distancias que hay entre dos puntos.	Regla, flexómetro, cinta métrica, cuenta kilómetros, calibrador,…	Km  Hm  Dam  m  dm  cm  mm
3	El área. Se trata de la superficie acotada de un recinto.	Regla, flexómetro, cinta métrica, cuenta kilómetros, calibrador,…	Km2  Hm2  Dam2  m2  dm2  cm2  mm2
4	El volumen. Es el espacio tridimensional ocupado por un cuerpo específico, mensurable en centímetros cúbicos (cm3).	Regla, flexómetro, cinta métrica, cuenta kilómetros, calibrador,…	Km3  Hm3  Dam3  m3  dm3  cm3  mm3
5	La capacidad. Mide lo que cabe dentro de un recipiente.	Jarras medidoras, probetas, pipetas, buretas, jeringas, etc…	Kl   Hl  Dal  l  dl  cl  ml
5	La masa. La cantidad de materia que contiene un objeto se mide como un valor fijo a través del sistema métrico o anglosajón de unidades: gramo, kilogramo, tonelada, libra, etc.	Balanza, báscula (las hay de muchos tipos).	Tm   Qm   Mag   Kg   Hg   Dag   g   dg   cg   mg
4	El tiempo. Duración de un hecho o situación.	Reloj, cronómetro	Siglo Año  Mes   Día   Hora   Minuto   Segundo…
5	La frecuencia. Mide el número de repeticiones de un fenómeno o suceso periódico por unidad de tiempo transcurrido.	Frecuencímetro	Su unidad son los hercios (Hz), que responden a la formulación 1Hz = 1/s, es decir, una repetición por segundo.

SOLUCIONES GRUPOS INTERACTIVOS 15-03-2019

ACTIVIDAD 1. FRACCIONES CON CARTONES DE HUEVOS

 ACTIVIDAD 2. EL TIEMPO Y LAS FRACCIONES

ACTIVIDAD 3. FRACCIONES Y ÁREAS DE COLOR

ACTIVIDAD 4. CÁLCULO DE VOLÚMENES

Cálculo de volumen. Ejercicio para fin de semana 9-03-2019

Busca en casa una cajita pequeña que debes traerte el lunes al colegio. Si sus caras son rectangulares la llamaremos ortoedro.

Mide (en centímetros) sus aristas ... (largo, ancho y alto) que te servirán para saber cuál es su volumen.

Volumen = largo x ancho x alto

Una vez calculado su volumen (en centímetros cúbicos), redondéalo y expresa su medida como fracción, como número decimal y como % de la unidad litro.

Por ejemplo, si nos hubiera dado 97 cm3, redondeamos hasta 100cm3, que sería 1/10 litro, 0,1 litros o el 10% de un litro.

¿Sabrías calcular cuáles serían las medidas de una caja grande en la que pudieras guardar 100 cajitas como la tuya?

FRACCIONES CON CARTONES DE HUEVOS

Aprendiendo fracciones con cartones de huevos y fichas de colores.

1º. Por grupos vamos a representar mediante cartones de huevos las siguientes fracciones, expresándolas también como número mixto y como número decimal.

GRUPO	FRACCIÓN	Nº MIXTO	DECIMAL
A	11/4
B	7/5
C	7/2
D	13/10

2º. Ordenar las fracciones de mayor a menor reduciéndolas a común denominador. Comprobar el resultado mediante el número decimal y su representación gráfica mediante los cartones de huevos.

3º. Resuelve las siguientes operaciones 

a)     A + B =

b) C + D  =

c) A- B =

d) C - D =

e) A + B + C + D =

f) A- B + C - D =

4º Resuelve gráficamente las mismas operaciones del ejercicio anterior.

5º. Otros problemas a resolver gráficamente con cartones de huevos:

a)      Tengo una finca de 20 hectáreas. He sembrado la cuarta parte de trigo, dos quintas partes de girasol y el resto la he dejado de barbecho (descanso). Indica las hectáreas que corresponden a cada cultivo y a barbecho.  

b)      Un embalse estaba lleno a finales de mayo. En el mes de junio se consumieron 3/10 de sus reservas y a finales de julio solo quedaba la mitad. ¿Qué fracción del embalse se consumió durante el mes de julio?

c)       Un empleado de mantenimiento utiliza 2/3 de un bote de pintura para pintar la valla de un chalé, y 2/5 de lo que le quedaba para pintar el cobertizo del jardín. Finalizada la tarea, aún le quedan 2 kilos de pintura. ¿Cuánto pesaba el bote de pintura antes de empezar?

d)      Ejercicios de la página 147 (del 36 al 44).

Las fracciones en distintas situaciones

Si aplicamos una misma fracción en distintas situaciones, aún siendo la misma fracción representa a conceptos totalmente distintos. No es lo mismo una botella de vino de 3/4 litros, que 3/4 de hora, que tener realizado los 3/4 de una tarea... Aquí vemos a las fracciones en distintos ámbitos:

Un rectángulo (una parcela).

Un agricultor ha sembrado de lechugas las tres séptimas partes de una parcela que tiene 50 metros de ancho por 140 metros de ancho. ¿Qué superficie ha sembrado? ¿Qué parte de la parcela le queda todavía libre?

Un círculo (una tarta).

Un negocio vende tartas de manzana. Si la fabricación de la tarta cuesta 20€ y la quiere vender en doce porciones ganando un total de 10 euros. Dibuja la tarta (15 cm de diámetro) con las doce porciones coloreando una de ella de amarillo. Señala cuánto sería el precio de cada porción.

Una línea (una distancia).

Un ciclista está haciendo una etapa que tiene 180 Km. El primer avituallamiento se sitúa a los 60Km, pincha en el Km 100, se cae en el km 150 y abandona.

Señala la fracción o parte de la carrera en la que se sitúa el avituallamiento, en el que tiene la avería y en el que abandona. ¿Qué parte de la carrera le quedaba todavía?

Un tiempo.

Tomando una hora como unidad, indica la fracción que representa los tiempos siguientes:

a)       Media hora           

b)      Tres cuartos de hora          

c)       Una hora y cuarto       

d)      Doce minutos

e)      Una hora y veinticinco minutos

f)        3,7 horas

g)       1,45 horas

h)      1h 20 minutos 30 segundos

Un dinero.

He comprado una bicicleta por 400€ pero he tenido que pagar el Impuesto del Valor Añadido IVA (que es el 21/100 del precio de la compra). ¿Cuánto he tenido que pagar al final?.

Si hubiera comprado la bicicleta con una rebaja del 25% (25/100) sobre el precio final después del impuesto, ¿Cuánto habría pagado? ¿Cuánto dinero me habría ahorrado?

Un grupo de elementos.

Averigua el equipo favorito de fútbol de tus compañeros y expresa el resultado de tu encuesta mediante fracciones.

La expresión del resultado de una tarea.

Un equipo de baloncesto ha colado 24 canastas de 120 intentos. ¿Cuál ha sido la fracción que representa a los aciertos? ¿Cuál ha sido la fracción que representa a los errores? ¿Cuál ha sido el % de aciertos y el % de errores?

El azar o estudio de probabilidades.
Indica la probabilidad de que al tirar un dado jugando al parchís obtengas el cinco para poder sacar una ficha.

La gastronomía.

Aquí puedes ver una propuesta de receta para hacer gazpacho, Se incluyen sus ingredientes y la cantidad que tenemos que poner de cada uno. Posteriormente sólo tenemos que triturar muy bien para poder disfrutar de un alimento rico y muy saludable,

1 kilo tomates rojos y maduros, 15 g dientes ajo, 20 g cebolla, 50 g pimiento verde, 70 g pepino, 30 g vinagre,    15 g cucharadita sal, 70 g aceite de oliva, 80 g pan y 150 g (150 ml) de agua,

Expresa en una tabla la composición del gazpacho indicando la fracción el número decimal y el % de  cada uno de sus ingredientes.